How To Use Pythagorean Identities
Pythagorean identities are formulas, derived from Pythagorean Theorem, that allow u.s.a. to find out where a indicate is on the unit circle. Learn the tricks and tips on how to use the unit circle to derive and prove the Pythagorean identities tin be hard.
What are the Pythagorean identities?
An identity in mathematics is an equation that is ever truthful. The Pythagorean identities all involve the number i and its Pythagorean aspects can be clearly seen when proving the theorems on a unit circle.
Pythagorean identities
We are going to explore the Pythagorean identities in this question. You may refer to the below formula sheet when dealing with the three Pythagorean identities.

Allow'due south explore the Pythagorean identities. The first of these three states that sine squared plus cosine squared equals one. The second ane states that tangent squared plus one equals secant squared. For the terminal one, it states that one plus cotangent squared equals cosecant squared.
In the post-obit question, we're going to endeavour to use a unit circle to bear witness the starting time Pythagorean identity: sine squared plus cosine squared equals 1.
Pythagorean identities examples
Question:
Use the unit circle to derive the Pythagorean Identity:
How practise we begin? Do you remember the backdrop of a unit circle? We've covered the unit circle in the previous department. To rapidly epitomize, a unit circle is just a circle with radius of i unit, i.e. the radius must equal one.

Refer to the higher up prototype. We'll identify a point on the circle at X,Y. Here, the X coordinate is Ten and the Y coordinate is Y.
From this point, let's describe a perpendicular line to the Ten axis. Nosotros will be focusing on this triangle.
In the above epitome, accept a moment to recall what ? means. It's actually the reference angle, right? It is one of the most of import angles in trigonometry.
In the reference bending, what does it mean if the X coordinate equals 10? It means that the length of the X segment is Ten. In a similar sense, if the Y coordinate is Y, that means the length of the vertical segment of the triangle would be Y.
Let's demonstrate this with bodily numbers to illustrate that concept.
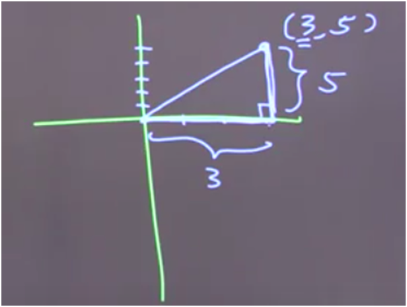
In the to a higher place example, there'southward a point called iii,5. If we draw a triangle, the 3 depicts the X coordinate. This means that the length of this segment is 3. Now, if the Y coordinate is 5, what does that hateful? The length of the vertical segment in the triangle must be five.
Going dorsum to the previous unit circle illustration, let'due south focus on the right-angled triangle and apply the Pythagoras theorem. What is the Pythagoras theorem? The Pythagoras tells us that X squared plus Y squared equals to the hypotenuse squared. The hypotenuse in this case is one, since we're using a unit circle. So here we take X squared plus Y squared equals one squared.
One neat thing about the unit of measurement circle is that its X coordinate can too be represented in terms of the angle theta. The Ten coordinate tin be represented as cosine theta, while its Y coordinate can be represented as sine theta. Continue in mind that this is only for a unit of measurement circle. So for whatsoever point on the unit of measurement circle: the X coordinate tin be represented as cosine theta; the Y coordinate tin can be represented equally sine theta.

Through using the unit circumvolve, the answer becomes very obvious. One squared is just one. The X coordinate can also exist represented every bit cosine theta. The Y coordinate can exist represented equally sine theta. And voila! Nosotros are done. From the unit of measurement circumvolve, we've successfully proved that cosine squared plus sine squared equals one, tackling one out of 3 Pythagorean identities.
How To Use Pythagorean Identities,
Source: https://www.studypug.com/trigonometry-help/pythagorean-identities
Posted by: hiltnore1993.blogspot.com


0 Response to "How To Use Pythagorean Identities"
Post a Comment